Unity シェーダーを学ぶ

【Unity Shader入門④】Shader GraphとShaderLab(HLSL)でグラデーションを作る

前回の記事では、Shader LabによるUnlitシェーダーについて解説しました。

今回の記事ではShader GraphおよびShader Labを用いて、グラデーションの効果を作ってみましょう。

グラデーションなんてすぐ作れると思っていても、初心者には難しかったりします。

新しいノードや考え方とか出てくるのでしっかり学んでいきましょう！

 

【前提環境】

Unityバージョン：6000.0.23f1

Shader Garphバージョン：17.0.3

 

目次
  1. Shader Graphでグラデーションを作る
  2. ShaderLab＋HLSLでグラデーションを作る
  3. まとめ

Shader Graphでグラデーションを作る

さてこれからShader Graphでオブジェクトの表面をグラデーションカラーにしてみましょう。

最終的なアウトプットは下記ポストのようなグラデーションです。

 

記事を読み進める前に自分で作ってみようと思う人は是非チャレンジしてください！

それでは解説始めます！

今回Unlitシェーダーを使い、下記のノードを使った実装例を示します！

  • Normal Vector
  • Normalize
  • Dot Product
  • Remap

Shader Graphの全体像

まずは全体像から見ると下記の図のようになります。

このシェーダーグラフはデフォルトのLit Shader Graphを元に作っています。

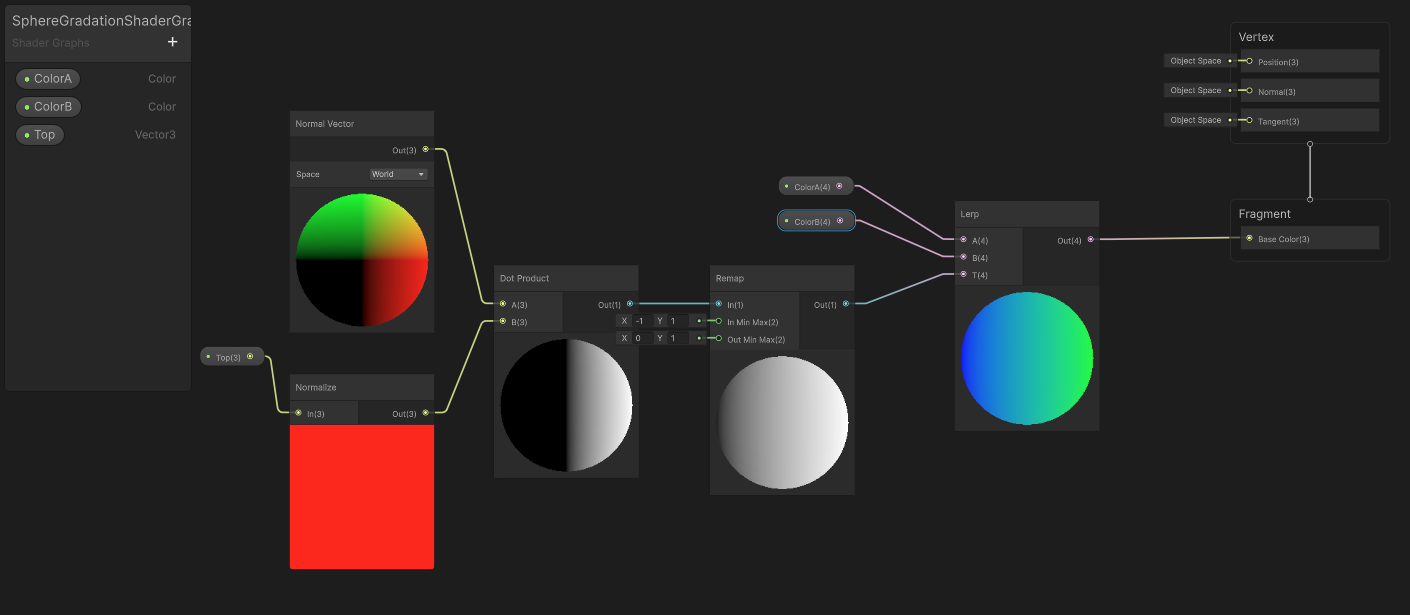
Unity Shader Graph グラデーション

インスペクター上で色を２色（ColorAとColorB）指定し、グラデーションのスタート位置をVector3型（Top）で示しています。

ノードの繋ぎ方をテキストで書くと下記のようになります。

  1. TopをNormalizeノードの入力に繋ぐ。
  2. Dot Productノードの入力AにはNormal Vectorノードの出力を、入力BにはNormalizeノードの出力を繋ぐ。
  3. Remapノードの入力にDot Productの出力をつなぎ、In Min Maxを（-1, 1）に、Out Min Maxを（0, 1）にする。
  4. Lerpノードの入力AとBにそれぞれColorAとColorBを繋ぎ、Remapの出力をTに繋ぐ。
  5. Lerpノードの出力をBase Colorに繋ぐ。

次に各ノードで何を行なっているかの解説をしてきます。

Normalizeノードは入力を正規化する

Normalizeノードでは入力されたベクトルの長さを1にするノードです。

プログラム的に書くと、sqrt(x^2 + y^2 + z^2)が1になるように調整した(x, y, z)を返します。

仮に(0.1, 0, 0)が入力されたら( 1, 0, 0 )が出力され、( 10, 0, 0 )が入力されても( 1, 0, 0)が出力されると言うことですね。

今回NormalizeしているTopという変数は、球の中心から球の表面の１点をに向けたベクトルがTopになり、その１点がColorAの一番濃い部分を表しています。

 

Normal Vectorノードは法線ベクトルのこと

Normal Vectorノードは読んで字の如く、法線ベクトルです。

オブジェクトの各頂点の法線ベクトルから、描画するピクセルの位置で補間した法線ベクトルが出力されます。

今回の例で言うと、球体の法線は球体の表面と直行するベクトルとなります。

 

Dot Productノードは2つのベクトルの内積

Dot Productノードは入力されたベクトルの内積を出力します。

と言っても、内積って何？って調べると、数式が出てきてコサインがどうのと出てきます。

ただその式の表すところは、「２つのベクトルの向きの一致度」を表しています。

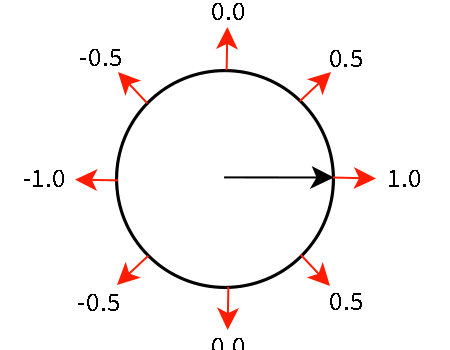
今回の例では、下記の黒い矢印がTopを赤い矢印が法線ベクトルを表している断面図で説明すると、２つのベクトルの一致度として-1.0から1.0の値が出力されることになります。

シェーダーグラフで見ると、1.0のところが白くなり、0.0以下のところが全部黒くなってますね（見た目では黒くなっていますが、値としては-1.0〜1.0になっています）。

Unity Shader Graph Dot Product

 

Remapで0〜1の範囲に修正する

Remapノードは入力した値を、入力値の範囲から出力値の範囲の値にしてくれます。

今回の例では入力値の範囲は-1.0〜1.0です。

この範囲の値を0.0〜1.0の範囲の値に変更しています。

つまり、仮に-1.0が入力されたら0.0を出力し、0.0が入力されたら0.5を出力し、1.0が入力されたら1.0を出力すると言うことです。

そのためシェーダーグラフ上では、0〜1の値が出力されて白から黒に向かってグラデーションが描かれてますね！

 

Lerpノードでグラデーションを作る

そしてLerpノードで二つの色を補間した値を出力するので、Base Colorに繋げてオブジェクトの色を変えています。

Lerpノードってなんだっけ？と思った方はこちらの記事をご覧ください。

 

ShaderLab＋HLSLでグラデーションを作る

次に、さっきのShader GraphをShaderLabで作ってみましょう。

私が作ったのは下記のようになります。

こちらもご自分で書いてみようと言う方はここで止めて、チャレンジしてみてください！

 

ShaderLabによるグラデーションの全体像

Shader "Unlit/SphereGradationShaderLab"
{
    Properties
    {
        _ColorA ("ColorA", Color) = (1,1,1,1)
        _ColorB ("ColorB", Color) = (0,0,0,1)
        _Top    ("Top", Vector) =  (1.0, 0.0 ,0.0)
    }
    SubShader
    {
        Tags { "RenderType"="Opaque" }
        Pass
        {
            CGPROGRAM
            #pragma vertex vert
            #pragma fragment frag

            #include "UnityCG.cginc"

            struct appdata
            {
                float4 vertex : POSITION;
                float3 normal : NORMAL;
            };

            struct v2f
            {
                half3 normal : TEXCOORD1;
                float4 vertex : SV_POSITION;
            };

            float4 _ColorA;
            float4 _ColorB;
            float3 _Top;

            v2f vert (appdata v)
            {
                v2f o;
                o.vertex = UnityObjectToClipPos(v.vertex);
                o.normal = v.normal;
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                float3 normalTop = normalize(_Top);
                float4 dotProduct = dot(normalTop, i.normal);

                float2 InMinMax = float2(-1, 1);
                float2 OutMinMax = float2(0, 1);

                float remap = OutMinMax.x + (dotProduct - InMinMax.x) * (OutMinMax.y - OutMinMax.x) / (InMinMax.y - InMinMax.x);
                return lerp(_ColorA, _ColorB, remap);
            }
            ENDCG
        }
    }
}

 

シェーダーの処理の流れ自体は、Shader Graphで説明したものと同じです。

ここではShaderLabでどのように実装しているか解説します。

 

ShaderLabの解説

法線ベクトルの扱い

下記は法線ベクトルの部分のみを抽出したものです。

    SubShader
    {
        Pass
        {
            struct appdata
            {
                float3 normal : NORMAL;
            };

            struct v2f
            {
                half3 normal : TEXCOORD0;
            };

            v2f vert (appdata v)
            {
                v2f o;
                o.normal = v.normal;
                return o;
            }

            fixed4 frag (v2f i) : SV_Target
            {
                float3 normalTop = normalize(_Top);
            }
            ENDCG
        }
    }

今回は各ピクセル単位の法線ベクトルが必要です。

そのためNORMALセマンティクスによりGPUから入力を受け付け、頂点シェーダーを通してフラグメントシェーダーに法線ベクトルの情報を入れる必要があります。

 

ビルトインのメソッドの有無

Shader GraphからShaderLabに変換するにあたり、ビルトインメソッドである下記のメソッドを使用しました。

  • normalize
  • dot
  • lerp

一方で、Remapノードに対応するメソッドはありませんので、自分で対応する処理を書かなければなりません。

とはいえ、対応する処理はUnityの公式マニュアルに記載しているのでそれを利用すれば書けます。

このようにビルトインで用意されている便利なメソッドの有無については実装のたびに調べて書かなければならないのが大変ですね。

 

まとめ

今回の記事では、Shader GraphとShaderLab（HLSL）それぞれを用いて、グラデーション表現を実装する方法を解説しました。

新しいノード、ビルトインメソッドを学んで行きましたが、少しずつ新しいものを取り入れて表現の幅をどんどん広げていましょう！

次回はTimeノードを用いた動きのあるシェーダーについて解説します！

-Unity, シェーダーを学ぶ